In cooperative multi-agent support knowing (MARL), due to its on-policy nature, policy gradient (PG) techniques are normally thought to be less sample effective than worth decay (VD) techniques, which are off-policy Nevertheless, some current empirical research studies show that with correct input representation and hyper-parameter tuning, multi-agent PG can accomplish remarkably strong efficiency compared to off-policy VD techniques.
Why could PG techniques work so well? In this post, we will provide concrete analysis to reveal that in particular situations, e.g., environments with an extremely multi-modal benefit landscape, VD can be troublesome and result in undesirable results. By contrast, PG techniques with specific policies can assemble to an optimum policy in these cases. In addition, PG techniques with auto-regressive (AR) policies can discover multi-modal policies.
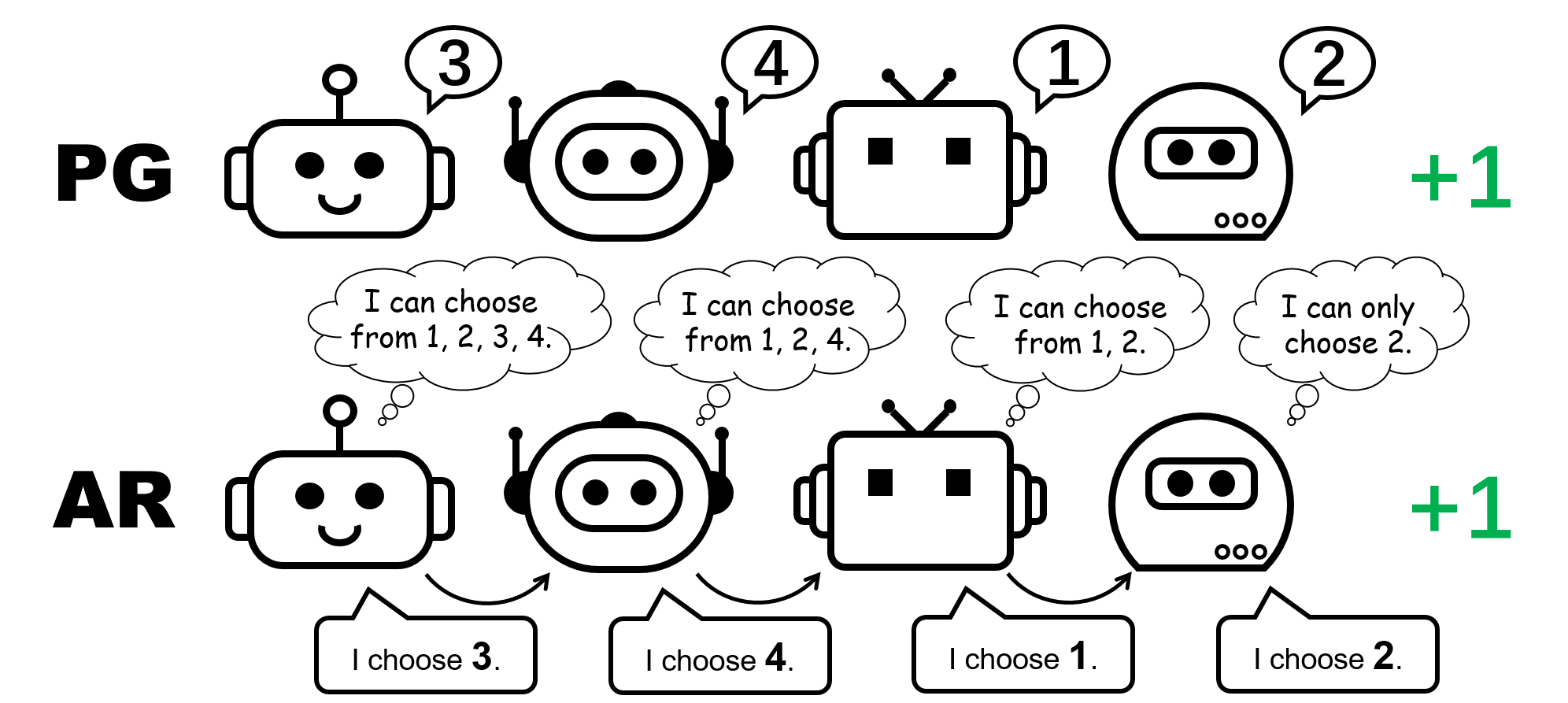
Figure 1: various policy representation for the 4-player permutation video game.
CTDE in Cooperative MARL: VD and PG techniques
Central training and decentralized execution ( CTDE) is a popular structure in cooperative MARL. It leverages worldwide details for more efficient training while keeping the representation of specific policies for screening. CTDE can be executed through worth decay (VD) or policy gradient (PG), resulting in 2 various kinds of algorithms.
VD techniques discover regional Q networks and a mixing function that blends the regional Q networks to a worldwide Q function. The mixing function is normally implemented to please the Individual-Global-Max ( IGM) concept, which ensures the ideal joint action can be calculated by greedily selecting the ideal action in your area for each representative.
By contrast, PG techniques straight use policy gradient to discover a specific policy and a central worth function for each representative. The worth function takes as its input the worldwide state (e.g., MAPPO) or the concatenation of all the regional observations (e.g., MADDPG), for a precise worldwide worth quote.
The permutation video game: a basic counterexample where VD stops working
We begin our analysis by thinking about a stateless cooperative video game, particularly the permutation video game. In an $N$- gamer permutation video game, each representative can output $N$ actions $ {1, ldots, N} $. Representatives get $+1$ reward if their actions are equally various, i.e., the joint action is a permutation over $1, ldots, N$; otherwise, they get $0$ benefit. Keep in mind that there are $N!$ symmetric ideal methods in this video game.
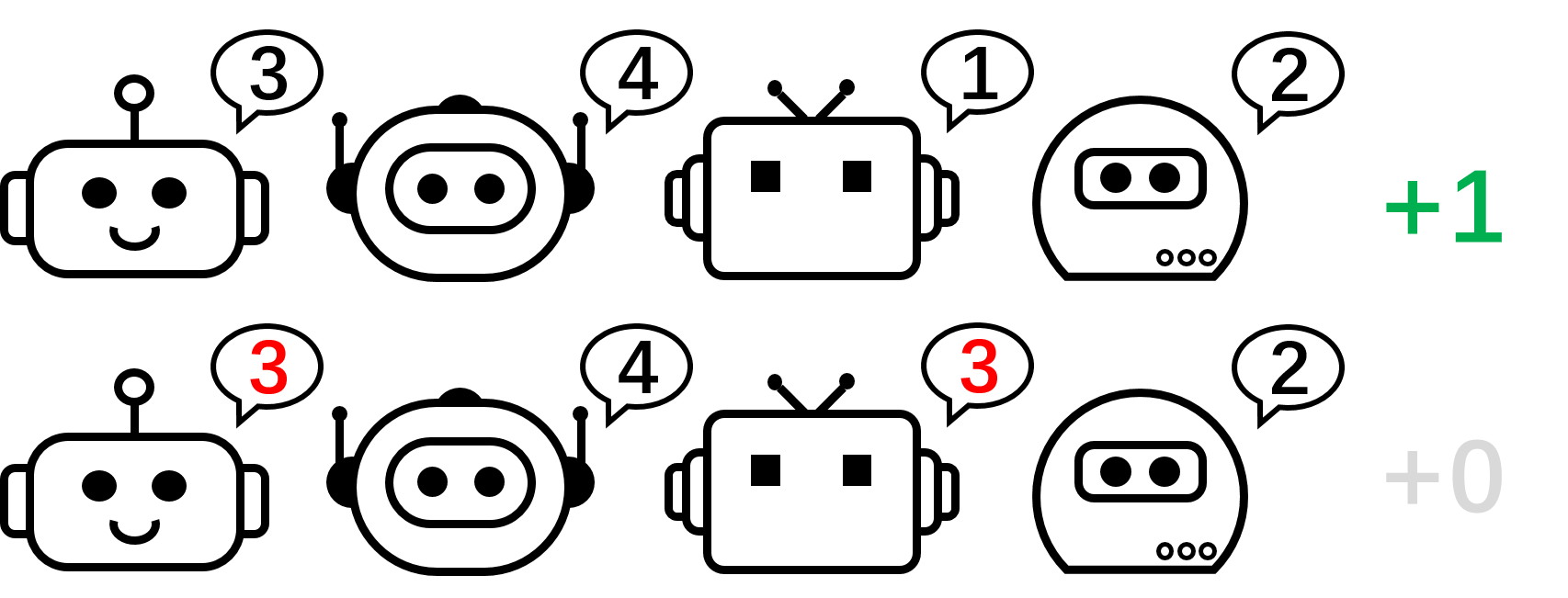
Figure 2: the 4-player permutation video game.
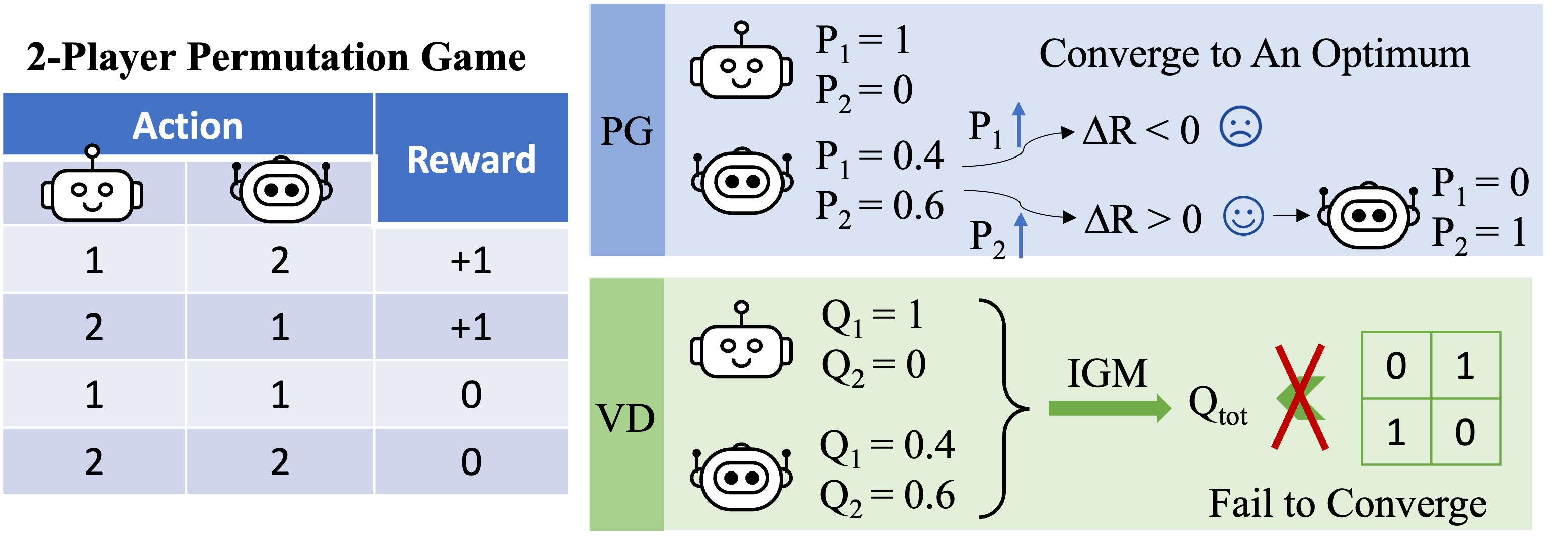
Figure 3: top-level instinct on why VD stops working in the 2-player permutation video game.
Let us concentrate on the 2-player permutation video game now and use VD to the video game. In this stateless setting, we utilize $Q_1$ and $Q_2$ to represent the regional Q-functions, and utilize $Q_textrm {kid} $ to represent the worldwide Q-function. The IGM concept needs that
[argmax_{a^1,a^2}Q_textrm{tot}(a^1,a^2)={argmax_{a^1}Q_1(a^1),argmax_{a^2}Q_2(a^2)}.]
We show that VD can not represent the benefit of the 2-player permutation video game by contradiction. If VD techniques had the ability to represent the benefit, we would have
[Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1)=1quad text{and}quad Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=0.]
If either of these 2 representatives has various regional Q worths (e.g. $Q_1( 1 )> > Q_1( 2 )$), we have $argmax _ {a ^ 1} Q_1( a ^ 1)= 1$. Then according to the IGM concept, any ideal joint action
[(a^{1star},a^{2star})=argmax_{a^1,a^2}Q_textrm{tot}(a^1,a^2)={argmax_{a^1}Q_1(a^1),argmax_{a^2}Q_2(a^2)}]
pleases $a ^ {1star} =1$ and $a ^ {1star} neq 2$, so the joint action $( a ^ 1, a ^ 2)=( 2,1)$ is sub-optimal, i.e., $Q_textrm {kid} (2,1)<< 1$.
Otherwise, if $Q_1( 1 )= Q_1( 2 )$ and $Q_2( 1 )= Q_2( 2 )$, then
[Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1).]
As an outcome, worth decay can not represent the benefit matrix of the 2-player permutation video game.
What about PG techniques? Private policies can certainly represent an optimum policy for the permutation video game. Additionally, stochastic gradient descent can ensure PG to assemble to among these optima under moderate presumptions This recommends that, although PG techniques are less popular in MARL compared to VD techniques, they can be more effective in particular cases that prevail in real-world applications, e.g., video games with numerous method techniques.
We likewise mention that in the permutation video game, in order to represent an optimum joint policy, each representative needs to pick unique actions. Subsequently, an effective execution of PG should guarantee that the policies are agent-specific. This can be done by utilizing either specific policies with unshared criteria (described as PG-Ind in our paper), or an agent-ID conditioned policy ( PG-ID).
PG surpasses existing VD techniques on popular MARL testbeds
Surpassing the easy illustrative example of the permutation video game, we extend our research study to popular and more practical MARL criteria. In addition to StarCraft Multi-Agent Difficulty ( SMAC), where the efficiency of PG and agent-conditioned policy input has actually been validated, we reveal brand-new lead to Google Research study Football ( GRF) and multi-player Hanabi Difficulty
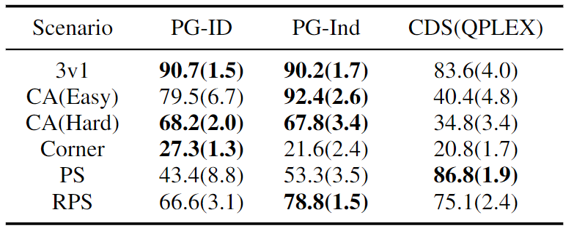
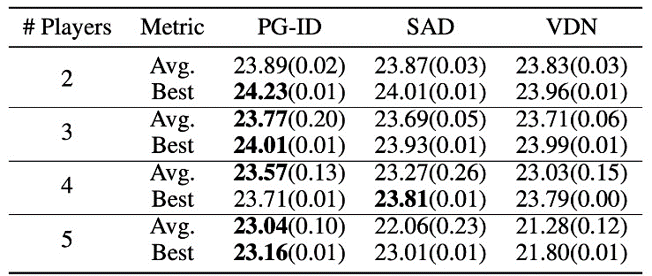
Figure 4: (left) winning rates of PG techniques on GRF; (right) finest and typical examination ratings on Hanabi-Full.
In GRF, PG techniques surpass the advanced VD standard ( CDS) in 5 situations. Surprisingly, we likewise see that specific policies (PG-Ind) without specification sharing accomplish similar, often even greater winning rates, compared to agent-specific policies (PG-ID) in all 5 situations. We assess PG-ID in the major Hanabi video game with differing varieties of gamers (2-5 gamers) and compare them to UNFORTUNATE, a strong off-policy Q-learning variation in Hanabi, and Worth Decay Networks ( VDN). As shown in the above table, PG-ID has the ability to produce outcomes similar to or much better than the very best and typical benefits attained by SAD and VDN with differing varieties of gamers utilizing the very same variety of environment actions.
Beyond greater benefits: finding out multi-modal habits through auto-regressive policy modeling
Besides finding out greater benefits, we likewise study how to discover multi-modal policies in cooperative MARL. Let’s return to the permutation video game. Although we have actually shown that PG can successfully discover an optimum policy, the method mode that it lastly reaches can extremely depend upon the policy initialization. Therefore, a natural concern will be:
Can we discover a single policy that can cover all the ideal modes?
In the decentralized PG solution, the factorized representation of a joint policy can just represent one specific mode. For that reason, we propose an improved method to parameterize the policies for more powerful expressiveness– the auto-regressive (AR) policies.

Figure 5: contrast in between specific policies (PG) and auto-regressive policies (AR) in the 4-player permutation video game.
Officially, we factorize the joint policy of $n$ representatives into the type of
[pi(mathbf{a} mid mathbf{o}) approx prod_{i=1}^n pi_{theta^{i}} left( a^{i}mid o^{i},a^{1},ldots,a^{i-1} right),]
where the action produced by representative $i$ depends upon its own observation $o_i$ and all the actions from previous representatives $1,dots,i-1$. The auto-regressive factorization can represent any joint policy in a central MDP. The just adjustment to each representative’s policy is the input measurement, which is a little bigger by consisting of previous actions; and the output measurement of each representative’s policy stays the same.
With such a very little parameterization overhead, AR policy considerably enhances the representation power of PG techniques. We mention that PG with AR policy (PG-AR) can at the same time represent all ideal policy modes in the permutation video game.

Figure: the heatmaps of actions for policies discovered by PG-Ind (left) and PG-AR (middle), and the heatmap for benefits (right); while PG-Ind just assemble to a particular mode in the 4-player permutation video game, PG-AR effectively finds all the ideal modes.
In more complex environments, consisting of SMAC and GRF, PG-AR can discover fascinating emerging habits that need strong intra-agent coordination that might never ever be discovered by PG-Ind.
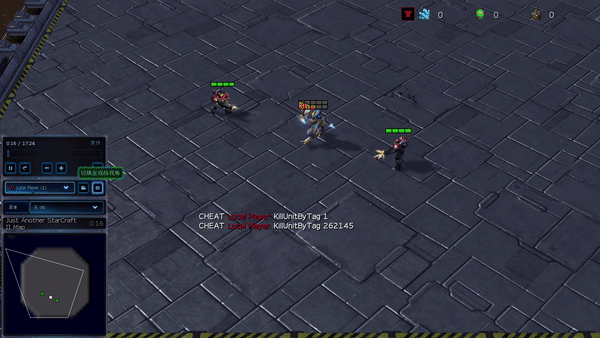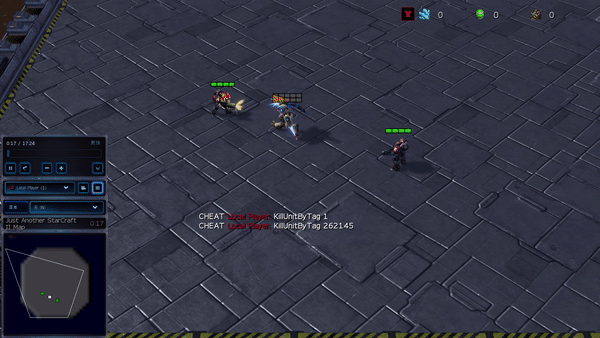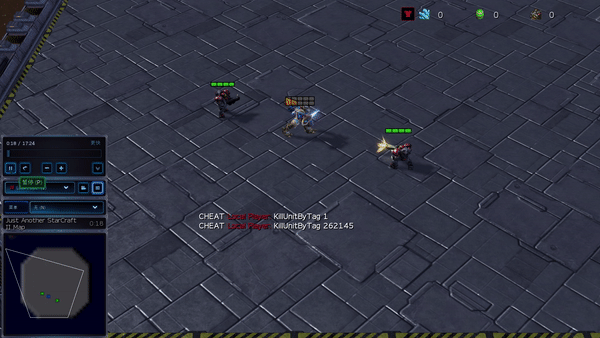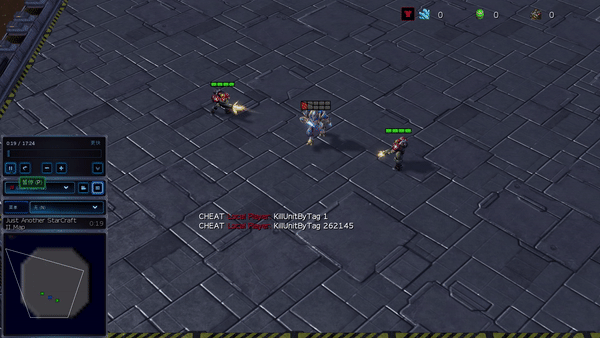
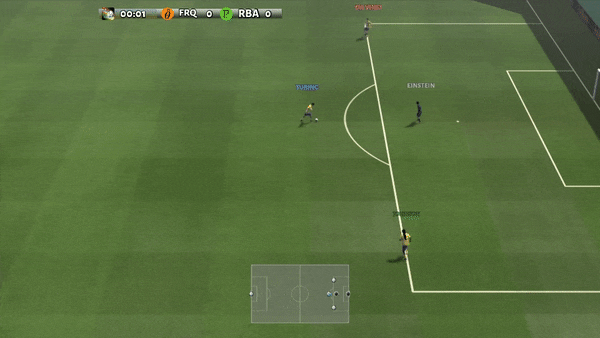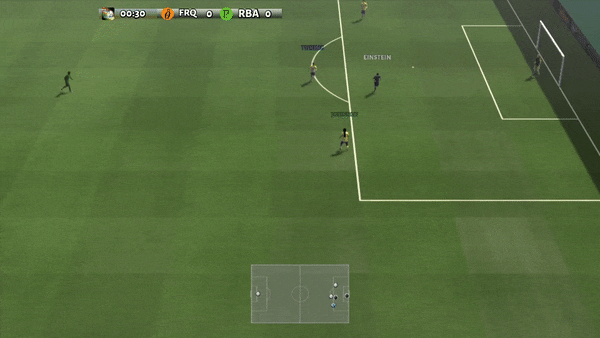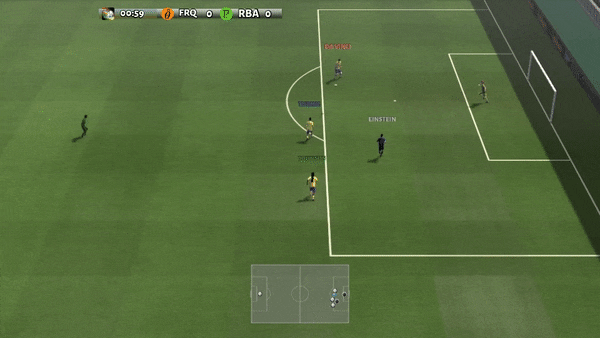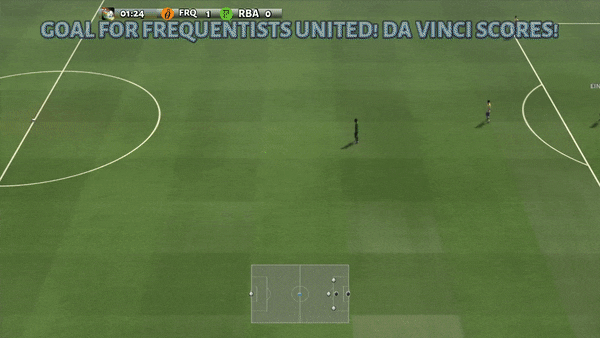
Figure 6: (left) emerging habits caused by PG-AR in SMAC and GRF. On the 2m_vs_1z map of SMAC, the marines keep standing and attack at the same time while guaranteeing there is just one assaulting marine at each timestep; (right) in the academy_3_vs_1_with_keeper circumstance of GRF, representatives discover a “Tiki-Taka” design habits: each gamer keeps passing the ball to their colleagues.
Discussions and Takeaways
In this post, we offer a concrete analysis of VD and PG techniques in cooperative MARL. Initially, we expose the constraint on the expressiveness of popular VD techniques, revealing that they might not represent ideal policies even in a basic permutation video game. By contrast, we reveal that PG techniques are provably more meaningful. We empirically confirm the expressiveness benefit of PG on popular MARL testbeds, consisting of SMAC, GRF, and Hanabi Difficulty. We hope the insights from this work might benefit the neighborhood towards more basic and more effective cooperative MARL algorithms in the future.
This post is based upon our paper: Reviewing Some Typical Practices in Cooperative Multi-Agent Support Knowing ( paper, site).