Deep neural networks have actually made it possible for technological marvels varying from voice acknowledgment to maker shift to protein engineering, however their style and application is however infamously unprincipled.
The advancement of tools and approaches to assist this procedure is among the grand obstacles of deep knowing theory.
In Reverse Engineering the Neural Tangent Kernel, we propose a paradigm for bringing some concept to the art of architecture style utilizing current theoretical advancements: very first style a great kernel function– typically a a lot easier job– and after that “reverse-engineer” a net-kernel equivalence to equate the selected kernel into a neural network.
Our primary theoretical outcome makes it possible for the style of activation functions from very first concepts, and we utilize it to develop one activation function that simulates deep (textrm {ReLU}) network efficiency with simply one surprise layer and another that comfortably exceeds deep (textrm {ReLU}) networks on an artificial job.
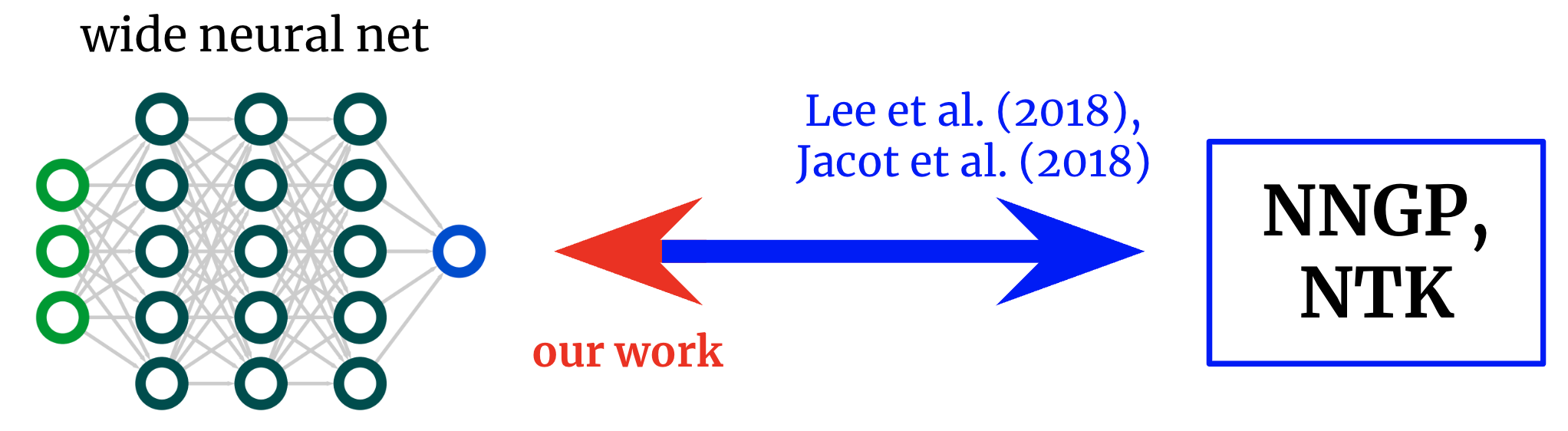
Kernels back to networks. Fundamental works obtained solutions that map from broad neural networks to their matching kernels. We get an inverted mapping, allowing us to begin with a preferred kernel and turn it back into a network architecture.
Neural network kernels
The field of deep knowing theory has actually just recently been changed by the awareness that deep neural networks typically end up being analytically tractable to study in the infinite-width limitation.
Take the limitation a particular method, and the network in truth assembles to a regular kernel technique utilizing either the architecture’s ” neural tangent kernel” (NTK) or, if just the last layer is trained (a la random function designs), its ” neural network Gaussian procedure” (NNGP) kernel
Like the main limitation theorem, these wide-network limitations are typically remarkably great approximations even far from limitless width (typically being true at widths in the hundreds or thousands), providing an impressive analytical manage on the secrets of deep knowing.
From networks to kernels and back once again
The initial works exploring this net-kernel correspondence offered solutions for going from architecture to kernel: offered a description of an architecture (e.g. depth and activation function), they offer you the network’s 2 kernels.
This has actually permitted excellent insights into the optimization and generalization of numerous architectures of interest.
Nevertheless, if our objective is not simply to comprehend existing architectures however to style brand-new ones, then we might rather have the mapping in the reverse instructions: offered a kernel we desire, can we discover an architecture that offers it to us?
In this work, we obtain this inverted mapping for fully-connected networks (FCNs), permitting us to develop easy networks in a principled way by (a) presuming a preferred kernel and (b) developing an activation function that offers it.
To see why this makes good sense, let’s very first imagine an NTK.
Think about a large FCN’s NTK (K( x_1, x_2)) on 2 input vectors (x_1) and (x_2) (which we will for simpleness presume are stabilized to the exact same length).
For a FCN, this kernel is rotation-invariant in the sense that (K( x_1, x_2) = K( c)), where (c) is the cosine of the angle in between the inputs.
Given That (K( c)) is a scalar function of a scalar argument, we can merely outline it.
Fig. 2 reveals the NTK of a four-hidden-layer (4HL) (textrm {ReLU}) FCN.
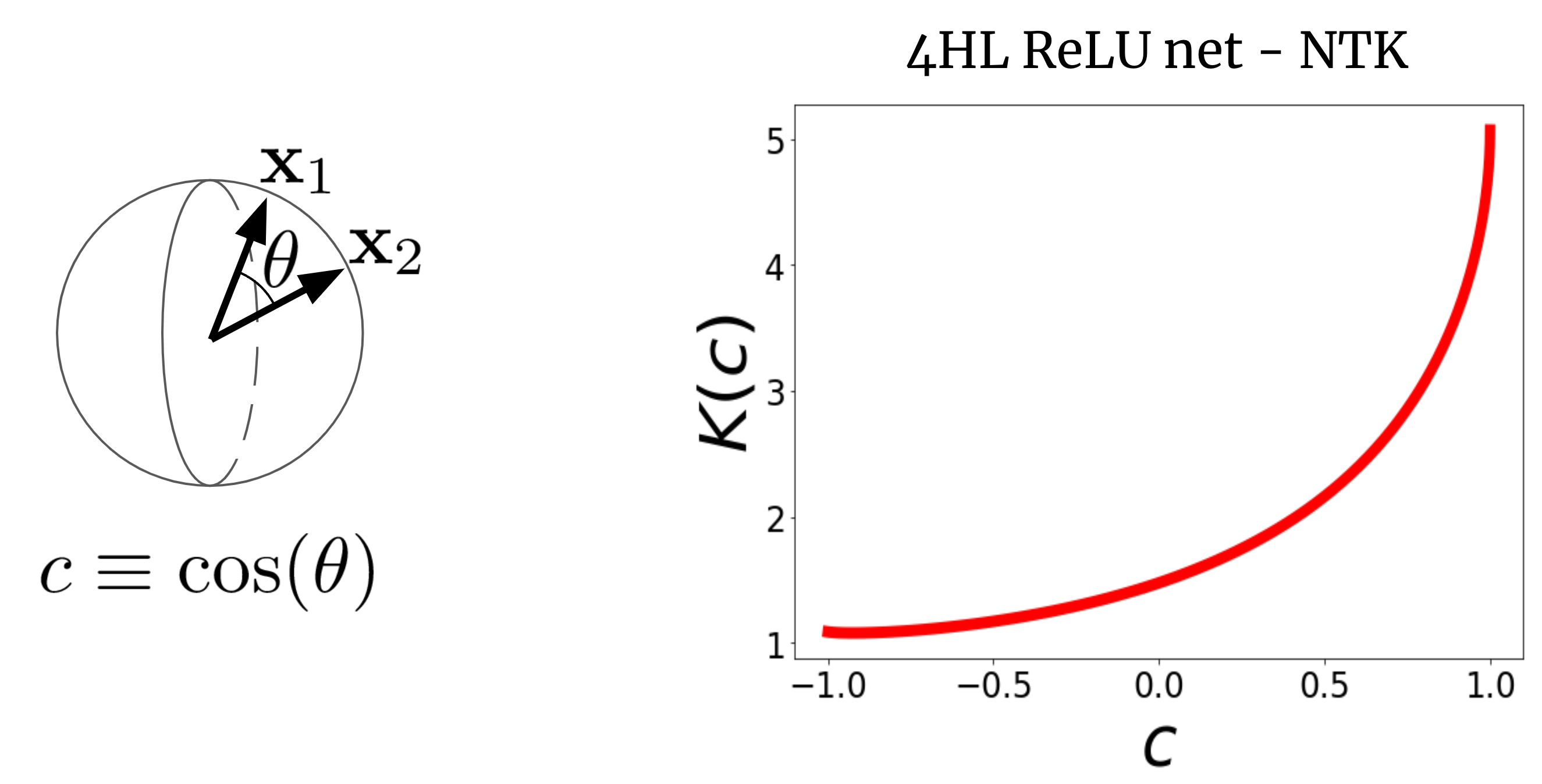
Fig 2. The NTK of a 4HL $textrm {ReLU} $ FCN as a function of the cosine in between 2 input vectors $x_1$ and $x_2$.
This plot really includes much details about the knowing habits of the matching broad network!
The monotonic boost indicates that this kernel anticipates closer indicate have more associated function worths.
The high boost at the end informs us that the connection length is not too big, and it can fit complex functions.
The diverging derivative at (c= 1) informs us about the smoothness of the function we anticipate to get.
Significantly, none of these realities appear from taking a look at a plot of (textrm {ReLU} (z))!
We declare that, if we wish to comprehend the impact of selecting an activation function (phi), then the resulting NTK is really more helpful than (phi) itself.
It therefore possibly makes good sense to attempt to develop architectures in “kernel area,” then equate them to the common hyperparameters.
An activation function for each kernel
Our primary outcome is a “reverse engineering theorem” that specifies the following:
Thm 1: For any kernel $K( c)$, we can build an activation function $tilde {phi} $ such that, when placed into a single-hidden-layer FCN, its infinite-width NTK or NNGP kernel is $K( c)$.
We offer a specific formula for (tilde {phi}) in regards to Hermite polynomials.
( though we utilize a various practical type in practice for trainability factors).
Our proposed usage of this outcome is that, in issues with some recognized structure, it’ll in some cases be possible to jot down a great kernel and reverse-engineer it into a trainable network with numerous benefits over pure kernel regression, like computational effectiveness and the capability to find out functions.
As an evidence of idea, we check this concept out on the artificial parity issue (i.e., offered a bitstring, is the amount odd and even?), instantly creating an activation function that significantly exceeds (text {ReLU}) on the job.
One surprise layer is all you require?
Here’s another unexpected usage of our outcome.
The kernel curve above is for a 4HL (textrm {ReLU}) FCN, however I declared that we can accomplish any kernel, consisting of that a person, with simply one surprise layer.
This indicates we can create some brand-new activation function (tilde {phi}) that offers this “deep” NTK in a shallow network!
Fig. 3 shows this experiment.
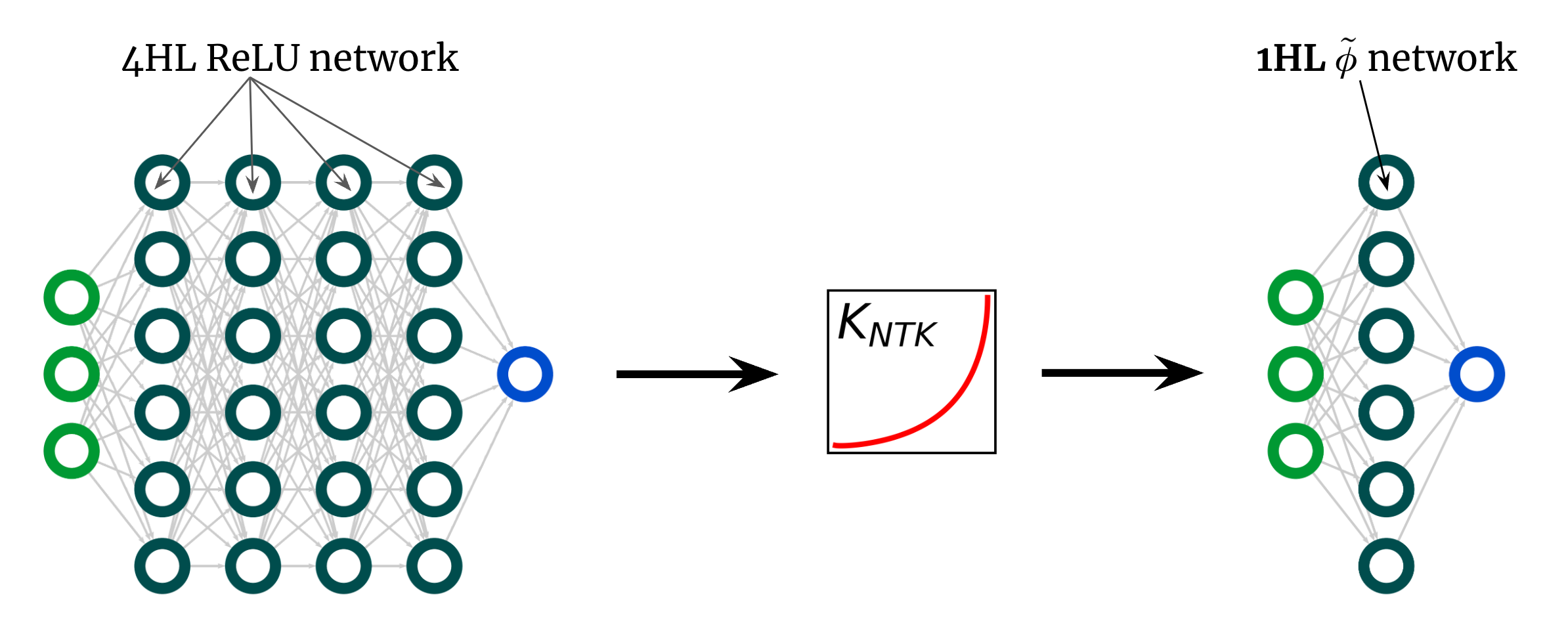
Fig 3. Shallowification of a deep $textrm {ReLU} $ FCN into a 1HL FCN with an engineered activation function $tilde {phi} $.
Remarkably, this “shallowfication” really works.
The left subplot of Fig. 4 listed below programs a “simulate” activation function (tilde {phi}) that offers essentially the exact same NTK as a deep (textrm {ReLU}) FCN.
The ideal plots then reveal train + test loss + precision traces for 3 FCNs on a basic tabular issue from the UCI dataset.
Keep in mind that, while the shallow and deep ReLU networks have extremely various habits, our crafted shallow simulate network tracks the deep network practically precisely!
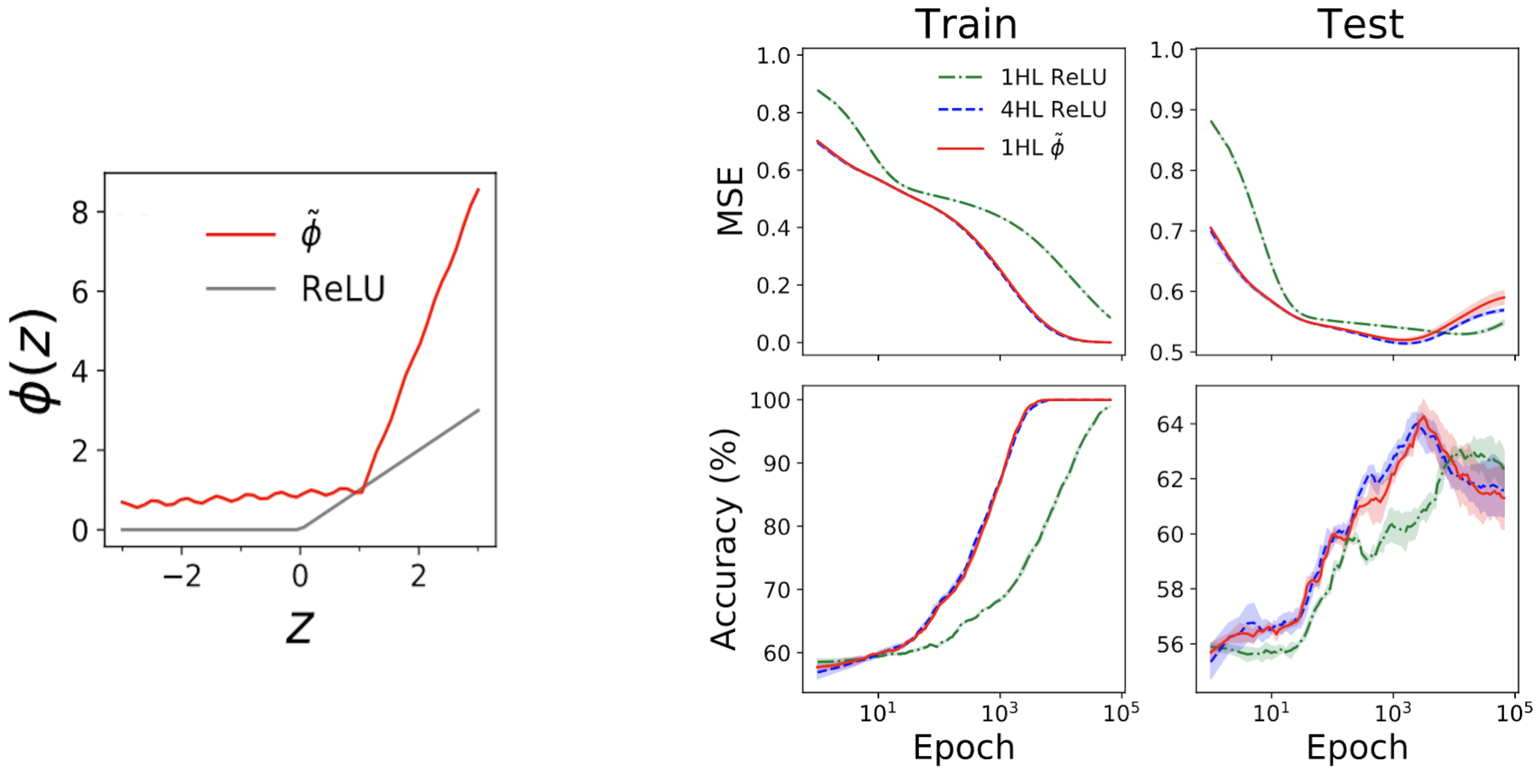
Fig 4. Left panel: our crafted “simulate” activation function, outlined with ReLU for contrast. Right panels: efficiency traces for 1HL ReLU, 4HL ReLU, and 1HL simulate FCNs trained on a UCI dataset. Keep in mind the close match in between the 4HL ReLU and 1HL simulate networks.
This is intriguing from an engineering point of view due to the fact that the shallow network utilizes less specifications than the deep network to accomplish the exact same efficiency.
It’s likewise intriguing from a theoretical point of view due to the fact that it raises basic concerns about the worth of depth.
A typical belief deep knowing belief is that much deeper is not just much better however qualitatively various: that deep networks will effectively find out functions that shallow networks merely can not.
Our shallowification outcome recommends that, a minimum of for FCNs, this isn’t real: if we understand what we’re doing, then depth does not purchase us anything.
Conclusion
This work includes great deals of cautions.
The greatest is that our outcome just uses to FCNs, which alone are hardly ever modern.
Nevertheless, deal with convolutional NTKs is quickly advancing, and our company believe this paradigm of developing networks by developing kernels is ripe for extension in some type to these structured architectures.
Theoretical work has up until now provided fairly couple of tools for useful deep knowing theorists.
We go for this to be a modest action in that instructions.
Even without a science to assist their style, neural networks have actually currently made it possible for marvels.
Simply envision what we’ll have the ability to make with them as soon as we lastly have one.
This post is based upon the paper “Reverse Engineering the Neural Tangent Kernel,” which is joint deal with Sajant Anand and Mike DeWeese We supply code to recreate all our outcomes. We ‘d be happy to field your concerns or remarks.